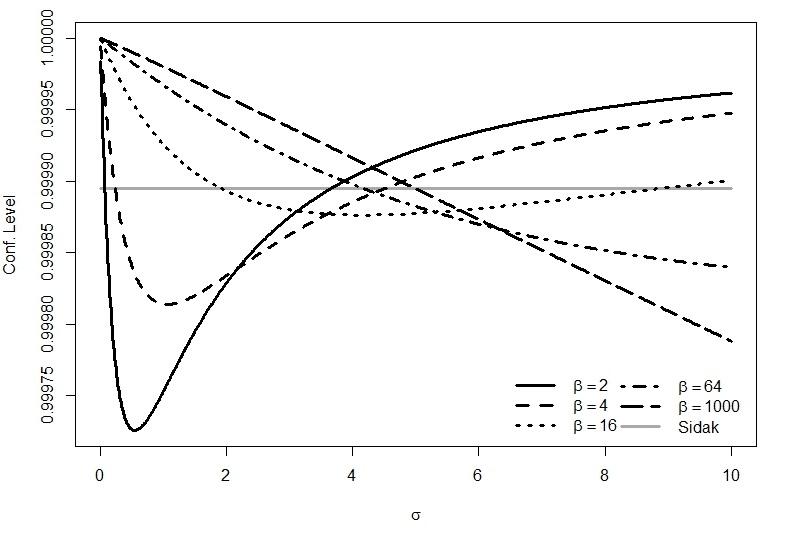
For a single-dimensional case, one usually attempts to minimize the average interval length
while maintaining the coverage probability at a higher-than-nominal level. When the number of
dimensions increases, the optimality problem in MIE looks like a simple extension of the single
dimensional case, at first glance, merely replacing the interval length and coverage probability
with "global" components. However, this turns out to be a more complex problem due to the
characteristics of multiplicity. In fact, it becomes necessary to allocate the individual levels to
their corresponding interval estimators simultaneously. Of course, I could assign a constant level
for every interval, following the Bonferroni or Sidak procedure. However, these approaches do not
reflect the characteristics of the individual intervals and thus result in wider global lengths.
I have investigated a decision-theoretic allocation procedure which assigns distinct levels to
interval estimators in order to minimize the global length. Through the allocation procedure,
I have reached a certain amount of reduction in the global length by adjusting the allocation
procedure compared to the z-based MIE. This allocation procedure is very general and widely
applicable to many different procedures.Bio Research Teaching Vitae
Dynamic Level Allocation Procedure
|
For a single-dimensional case, one usually attempts to minimize the average interval length
while maintaining the coverage probability at a higher-than-nominal level. When the number of
dimensions increases, the optimality problem in MIE looks like a simple extension of the single
dimensional case, at first glance, merely replacing the interval length and coverage probability
with "global" components. However, this turns out to be a more complex problem due to the
characteristics of multiplicity. In fact, it becomes necessary to allocate the individual levels to
their corresponding interval estimators simultaneously. Of course, I could assign a constant level
for every interval, following the Bonferroni or Sidak procedure. However, these approaches do not
reflect the characteristics of the individual intervals and thus result in wider global lengths.
I have investigated a decision-theoretic allocation procedure which assigns distinct levels to
interval estimators in order to minimize the global length. Through the allocation procedure,
I have reached a certain amount of reduction in the global length by adjusting the allocation
procedure compared to the z-based MIE. This allocation procedure is very general and widely
applicable to many different procedures. |
Median Interval Estimation in a Nonparametric Model
|
This work regards the classical problem of constructing interval estimators (IE) for the median in the
nonparametric measurement error model (NMEM). The novelty of the work is the derivation of optimal
equivariant IEs on subclasses of the class of all distributions, relying only on the Invariance Principle.
The performances of the developed IEs are compared to the current methods, including the T-statisticbased
IE and the Wilcoxon signed-rank statistic-based IE, arguably the two default methods in applied
work when the target of the estimation is the center of a distribution. Applications to a real car mileage
efficiency data set and Proschan's air-conditioning data set are demonstrated. Simulation studies to
compare the performances of the different IE methods were undertaken. The results indicate that the
sign-statistic based IE and the optimal IE focused on symmetric distributions satisfy the confidence
level requirement, though they tended to have higher contents; while two of the bootstrap-based IE
procedures and one of the developed adaptive IE tended to be a tad more liberal, but with smaller
contents. However, both the t-based and Wilcoxon signed-rank statistic-based IEs should not be used
under the NMEM, as they have degraded confidence levels and/or inflated contents. |
Multiple Interval Estimation with Thresholding
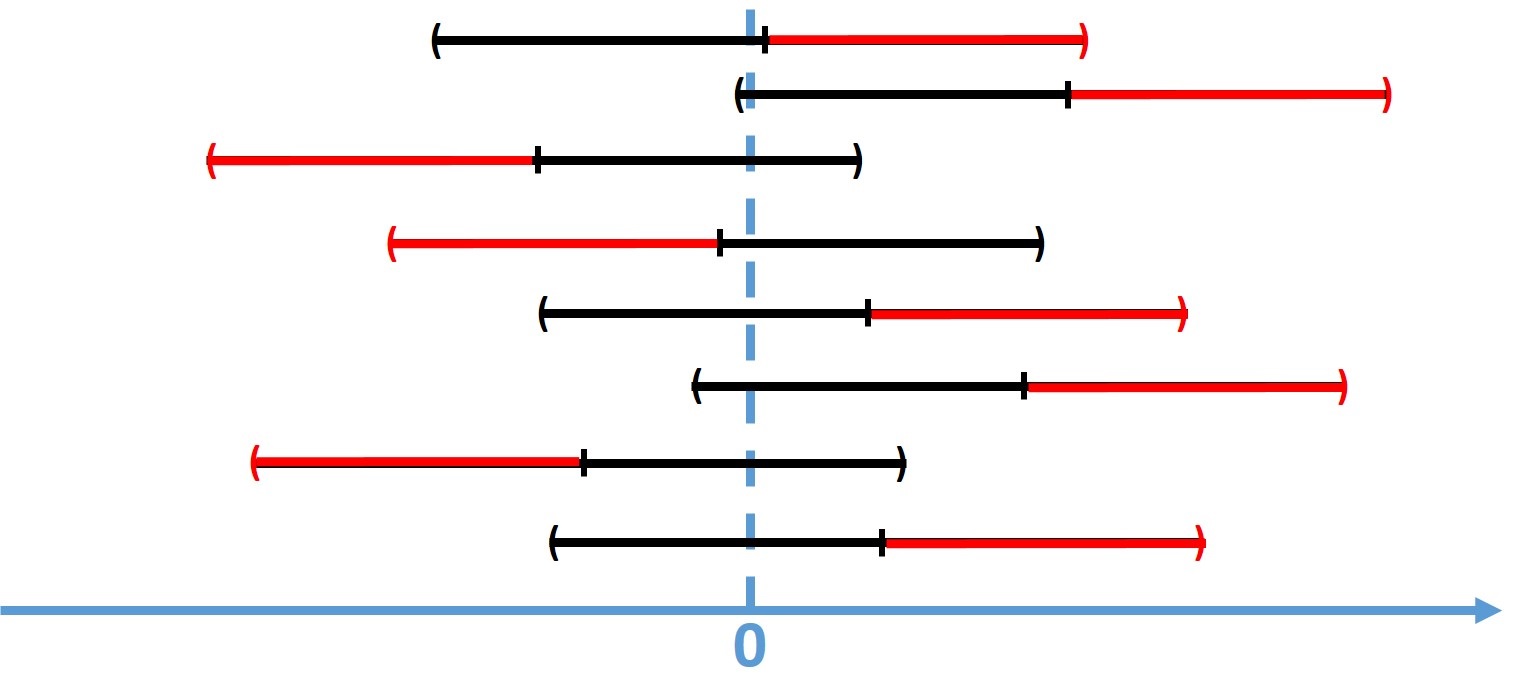The idea of a thresholding approach for an MIE is motivated by the desire to remove one side of some
IEs to minimize the global expected length. For example, if an MIE is constructed to compare a set
of two group means, then almost all zeros are covered by the inner tails of IEs. In such a situation,
a statistician would wish to remove the outer tails, since they
cause redundancy. The thresholding idea provides justification
for this removal process. However, it requires additional information
to set up the thresholds; thus, prior information is utilized
for the purpose. Then the corresponding performance quantities,
the expected length, and coverage probability can be summarized
by integrating them with respect to the prior distribution. The
resulting procedure is called Bayes MIE with Thresholding (BMIE
Thres), since the integration process is reminiscent of the derivation
of Bayes risk. Still, the procedure follows the Frequentist perspective in that the MIE is based
on the maximum likelihood estimator. In comparison to the classical z-based MIE, I have confirmed
considerable reductions in the global expected length when examining in-season baseball batting average
data and leukemia gene expression data. This means that the BMIE Thres provides better precision for
multiple parameter estimations. |
Multiple Interval Estimation for a Set of Heterogeneous Parameters
|
When estimating heterogeneous parameters with an MIE, one encounters difficulties in summarizing
the performance information due to the distinct characteristics of each parameter. In particular, the
expected lengths of the individual IEs require distinct measures with respect to the heterogeneous
parameters{this is like measuring apples by their circumference and bananas by their length. Therefore,
when the MIE combines these individual IEs, the global structure should involve logic to compare those
distinct measures to derive proper global performance quantities. To address this issue, I invoke the
Invariance Principle to assign groups to individual structures. Under certain conditions, the concept of
Haar measure provides the prior information for the parameter space. The resulting MIE, which is based
on the group structure, is called equivariant MIE with Haar measures (EMIE Haar). The advantage of
EMIE Haar is that the coverage probability and expected length be simplified by the Invariance Principle,
and the proper measures for the performance quantities can be derived from the Haar measure. As a
result, if group structures are available for different parameters with compatible Haar measures, the
EMIE Haar provides a coherent global structure to handle the heterogeneity. |