Practice Examination 01 (With Answers)

SCCC 312

(without using your notes)

Part A: A researcher is interested in studying the price per gallon of regular unleaded gasoline in the Metropolitan Columbia area. In particular, he is interested in the average or mean price of all the gas stations in Metro Columbia. To estimate this mean price, he decides to take a random sample of size 30 gas stations from Metro Columbia, and to determine their price per gallon of regular unleaded gasoline during a specified date.

1) Describe the population of study. (Answer: All gas stations in the Metropolitan Columbia area.)

2) Describe the variable(s) of interest. (Answer: Price per gallon of regular unleaded gasoline for the specified date.)

3) Describe the parameter of interest. (Answer: Mean price of unleaded gasoline for all the gas stations in Metro Columbia.)

4) Describe the sample in this study. (Answer: The 20 gas stations that were randomly chosen.)

5) Describe briefly how you might choose this sample of 30 gas stations. (Answer: Enumerate all the gas stations, number them, and then choose 20 among them using the computer.)

Part B: A random sample of 8 music CDs have the following playing times, in minutes.

72, 51, 67, 70, 50, 78, 46, 74

Using this data, compute the following sample statistics.

1) mean (Answer: 63.50)

2) median (Answer: 68.50)

3) first quartile (Answer: 51 )

4) third quartile (Answer: 74)

5) sample variance (Answer: S² = (12.49)^2)

6) sample standard deviation (Answer: S = 12.49)

7) Draw the 5-number summary (box plot) (Answer: See plot below.)

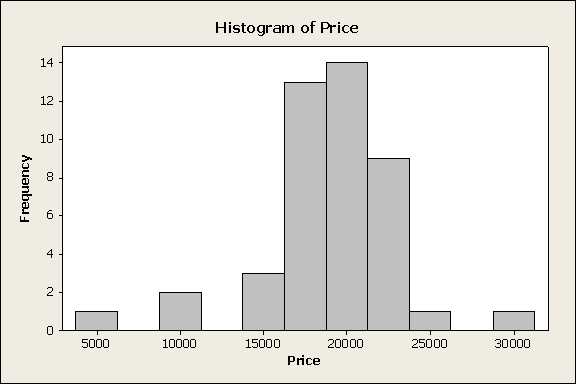
Part C: The following summaries are based on 44 car prices. These summaries were obtained using Minitab.

Stem-and-Leaf Display: Price

Stem-and-leaf of Price N = 44

Leaf Unit = 100

LO 56, 89, 99

5 14 59

5 15

7 16 04

12 17 29999

(12) 18 023456679999

20 19 29999

15 20 9999

11 21 599999

5 22 99

3 23 69

HI 291

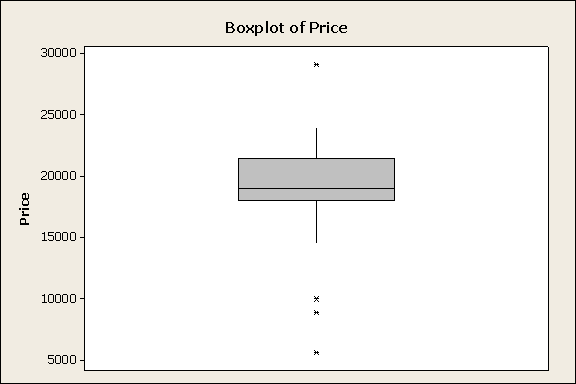
Descriptive Statistics: Price

Variable N N* Mean SE Mean StDev Minimum Q1 Median Q3 Maximum

Price 44 0 19023 598 3966 5600 17999 18999 21449 29150

1) How would you describe the shape of the histogram of the data set. (Answer: a little bit left-skewed, though also close to being symmetric.)

2) What percentage of car prices in this sample were at least $18999? (Answer: 50% since 18999 is the median)

3) What is the approximate percentage of car prices that were between 17999 and 21449? (Answer: 50% since this interval goes from the first quartile to the third quartile.)

4) What is the approximate percentage of observations that were between 19023 – (2)(3966) and 19023 + (2)(3966). Explain how obtained your answer. (Answer: Approximately 95% using the empirical rule and since the histogram is close to being symmetric. However, using Chebyshev’s we are guaranteed that there are at least 75% of all observations in this interval.)

5) Are there outliers in this data set? if so, what are they? (Answer: From the box plot, those corresponding to asterisks are otuliers.)

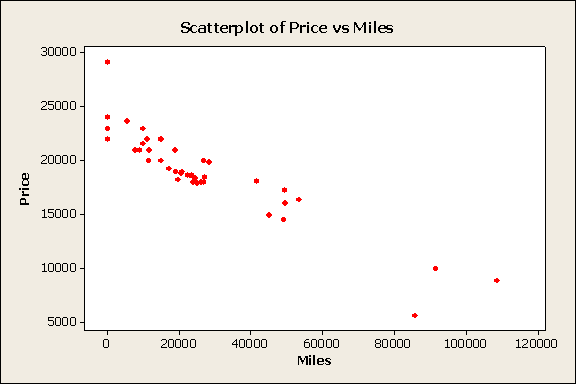
Part D: Aside from the price of the car, the current mileage of the car was also recorded. The scatter plot of the mileage and the price is given below.

In addition, we have the following information obtained from Minitab:

Correlations: Price, Miles

Pearson correlation of Price and Miles = -0.916

Regression Analysis: Price versus Miles

The regression equation is

Price = 22950 - 0.153 Miles

Predictor Coef SE Coef T P

Constant 22950.0 360.0 63.75 0.000

Miles -0.15345 0.01038 -14.78 0.000

S = 1611.34 R-Sq = 83.9% R-Sq(adj) = 83.5%

Use these information to answer the following questions.

1) Describe the type of association or relationship between mileage and price. Would you say that the relationship is linear? Justify your answer by citing the information you are using. (Answer: linear and negative. The correlation coefficient is -.916)

2) What is the value of the y-intercept of the prediction line? (Answer: 22950)

3) What is the value of the slope or regression coefficient of the prediction line? (Answer: -.153)

4) What is the value of the coefficient of determination? What is the importance of this value? (Answer: 83.9%. This measures the strength of the prediction line. It is the square of the correlation coefficient.)

5) Suppose that a car has current mileage of 22,000 miles. by using the prediction equation obtained above, what will be the predicted price of this car? (Answer: 22950 – (.153)(22000))

Part E: Consider the random experiment of tossing a fair coin 4 times. Based on this experiment, answer the following questions.

1) What is the sample space of this experiment? (Answer: S = {(HHHH), (HHHT), (HHTH), (HTHH), (THHH), (HHTT), (HTHT), (THHT), (HTTH), (THTH), (TTHH), (HTTT), (THTT), (TTHT), (TTTH), (TTTT)})

2) What are the probabilities of the outcomes in this sample space? What is your justification? (Answer: 1/16 each)

3) Let A be the event that the outcomes of the 4 tosses are identical. What is the probability of event A? (Answer: 2/16)

4) Let B be the event that the outcome has at least 3 heads in the outcome. What is the probability of event B? (Answer: 5/16)

5) Determine the probability that either A or B occurs. (Answer: 6/16)

6) Determine the probability that both A and B occur. (Answer: 1/16)

7) Are events A and B mutually exclusive? (Answer: No)

8) Are events A and B are independent? (Answer: No since P(AB) not equal to P(A)P(B))

9) Given that the first two tosses resulted in heads, what is the conditional probability that there will be exactly 1 tail in the outcome. (Answer: 2/4)